- Assoziativgesetz der Addition
- Beispiel für das Assoziativgesetz der Addition
- Assoziativgesetz der Multiplikation
- Beispiel für das Assoziativgesetz der Multiplikation
Als Assoziativgesetz bezeichnet man Rechenregeln, die bestimmen, in welcher Reihenfolge mehrere Rechnungen in einer Formel ausgeführt werden. Von besonderer Bedeutung für die Schule sind das Assoziativgesetz der Addition und das Assoziativgesetz der Multiplikation. Beide Gesetze werden bereits in der Grundschule gelernt und sollten von jedem Schüler ohne Probleme angewandt werden können.
Assoziativgesetz der Addition
Das Assoziativgesetz der Addition bezieht sich auf Formeln, in denen mehrere Additionen nacheinander durchgeführt werden. Es besagt, dass es keine Rolle spielt, welche der Additionen zuerst und welche zuletzt durchgeführt werden.
Als Formel ausgedrückt lautet das Assoziativgesetz der Addition:
Diese Formel zeigt den Fall, dass drei Zahlen a, b und c addiert werden. Hier kommen wir jedes Mal zum selben Ergebnis, egal in welcher Reihenfolge die Zahlen addiert werden. Es können also sowohl zuerst a und b, als auch b und c addiert werden, bevor die jeweils dritte Zahl addiert wird. Es ist sogar möglich, zuerst a und c zu addieren.
Die Klammern in der Formel geben die Reihenfolge der Rechnung an. Auf der linken Seite der Formel ist die Addition von b und c eingeklammert und wird deshalb vor der Addition mit a durchgeführt. Auf der rechten Seite ist die Addition von a und b eingeklammert und wird vor der Addition von c durchgeführt. Das Assoziativgesetz der Addition besagt, dass bei mehreren Additionen gleichgültig ist, um welche der Addition eine Klammer gesetzt ist und um welche nicht. Das Assoziativgesetz wird deshalb häufig auch „Klammergesetz“ genannt.
Beispiel für das Assoziativgesetz der Addition
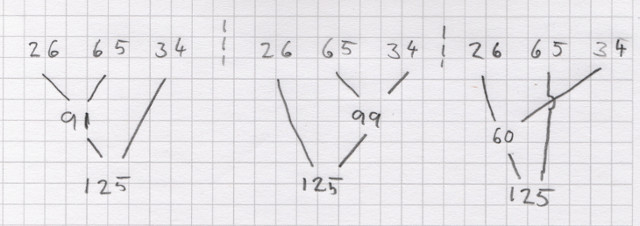
Ein Beispiel für das Assoziativgesetz der Addition ist die Berechnung von:
Hier können wir frei entscheiden, welche der beiden Zahlen wir zuerst addieren und welche wir als drittes addieren. So ergibt sich:
Wenn wir die Regeln des Assoziativgesetz der Addition als Baum darstellen, wird besonders deutlich, wie wir bei der Rechnung vorgehen können:
Assoziativgesetz der Multiplikation
Das Assoziativgesetz der Multiplikation gilt für Formeln, in denen mehrere Zahlen, bzw. Terme, nacheinander multipliziert werden. Es besagt, dass die Reihenfolge, in der die einzelnen Multiplikationen ausgeführt werden, keinen Einfluss auf das Ergebnis hat.
Als Formel ausgedrückt lautet das Assoziativgesetz der Multiplikation:
In dieser Formel werden die drei Zahlen a, b und c miteinander multipliziert. Auf der rechten Seite der Formel wird der Fall dargestellt, dass zuerst a und b miteinander multipliziert werden und das Ergebnis anschließend mit c multipliziert wird. Auf der linken Seite wird der Fall dargestellt, dass zuerst b und c miteinander und anschließend mit a multipliziert werden. Es wäre ebenso möglich zuerst a und c miteinander und anschließend mit c zu multiplizieren. Das Assoziativgesetz der Multiplikation besagt, dass alle Rechnungen dasselbe Ergebnis liefern.
Beispiel für das Assoziativgesetz der Multiplikation
Das Assoziativgesetz der Multiplikation können wir beispielsweise bei der Berechnung dieser Formel anwenden:
In welcher Reihenfolge wir die Faktoren multiplizieren spielt für das Ergebnis keine Rolle. Es gelten die drei Fälle:
Wie man leicht überprüfen kann, führen alle drei Rechnungen zu demselben Ergebnis, auch wenn die Faktoren jeweils in anderer Reihenfolge multipliziert wurden.
