Mit dem Differenzenquotient berechnet man die Steigung einer Funktion in einem bestimmten Abschnitt. Seine Bedeutung wird anschaulich klar, wenn man sich vorstellt, dass man zwei Punkte auf dem Graphen einer Funktion markiert und zwischen ihnen eine Gerade zeichnet. Die Steigung der Geraden entspricht dann der Steigung der Funktion vom ersten zum zweiten Punkt. Den Wert der Steigung erhält man über den Differenzenquotienten.
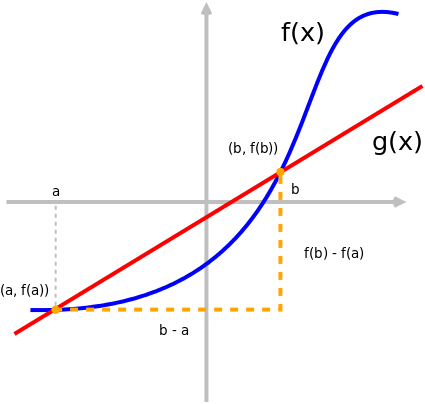
Formal ist die Steigung einer Funktion f vom Punkt (a,f(a)) zu einem zweiten Punkt (b,f(b)) definiert, als der Quotient der Differenz der beiden Funktionswerte und der Differenz der beiden Variablen. Daher auch der Name Differenzen-Quotient. Die Formel für den Differenzenquotienten lautet also:
Wenn wir zu einer gegebenen Funktion f und zwei Variablen a und b die Funktion g der Geraden berechnen wollen, die die beiden Punkte (a,f(a)) und (b,f(b)) verbindet, können wir wieder den Differenzquotienten nutzen und kommen so auf die Geradengleichung:
Eine solche Gerade, die zwei Punkte auf dem Graphen einer Funktion verbindet und den Graphen der Funktion an jedem der beiden Punkte schneidet, heißt Sekante.
Beispiele für den Differenzenquotient
Angenommen, wir haben die eine Funktion f mit dieser Funktionsgleichung:
Für diese Funktion, wollen wir die Steigung zwischen den beiden Punkten (2, f(2)) und (5, f(5)) berechnen.
Einsetzen der Werte in den Differenzenquotienten ergibt:
Die Gleichung für die zugehörige Sekante lautet:
Es handelt sich dabei also um eine Gerade mit der Steigung 7 und dem y-Achsenabschnitt -13.
Zusammenfassung Differenzenquotient
Der Differenzenquotient ist ein sehr nützliches Konzept in der Mathematik. Er ermöglicht es uns, eine Funktion an einem beliebigen Punkt zu bestimmen, ohne sie zu integrieren oder zu differentieren. Das ist besonders nützlich, wenn die Funktion sehr komplex ist und wir keine Antwort auf die Integration oder Differentiation erhalten können.
