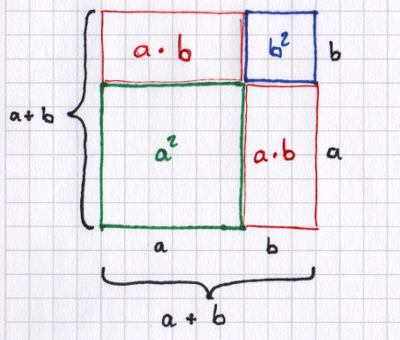
Bruchrechnen ist das Rechnen mit Bruchzahlen, bzw. Brüchen, die aus einem Zähler und einem Nenner bestehen. Alle Zahlen, die sich als Bruch darstellen lassen, gehören der Menge der rationalen Zahlen an. Das Bruchrechnen ist für weite Teile der Mathematik grundlegend.
| Formel |
Bedeutung |
 |
Addition von Brüchen mit gleichem Nenner |
 |
Addition von Brüchen mit unterschiedlichem Nenner |
 |
Multiplikation von Brüchen |
 |
Der Kehrwert eines Bruches |
 |
Division zweier Brüche |
Beim Bruchrechnen rechnet man mit den Teilen ganzer Zahlen. Das heißt, dass man nicht nur Aufgaben berechnet, in denen die natürlichen Zahlen vorkommen, sondern auch solche, in denen die sogenannten rationalen Zahlen benötigt werden. Bruchrechnen ist in vielen Zusammenhängen sinnvoll: Beispielsweise kann man mit seiner Hilfe ermitteln, wie man einen Kuchen aufteilt. Das geht oft ganz intuitiv, kann aber sehr nützlich sein, wenn man Bruchrechnen üben will. Will man beispielsweise einen Kuchen zu zweit essen, muss man ihn durch zwei teilen, also bekommt jeder einen halben Kuchen, will man ihn zu fünft essen, muss man ihn durch fünf teilen. Jeder bekommt jetzt ein Fünftel des Kuchens. Verzichtet aber einer auf sein Stück und gibt es stattdessen an einen Freund, kann dieser sogar zwei Fünftel des Kuchens essen. Diese praktische Anwendung der Bruchrechnung gehört zu den typischen Aufgaben im Bruchrechnen.
Eine Bruchzahl beschreibt eine Zahl als Quotient aus Zähler und Nenner. Der Bruchstrich hat dabei dieselbe Bedeutung wie das Geteilt-Zeichen. Oberhalb des Bruchstrichs steht dabei der Divident. Er wird in der Bruchrechnung als „Zähler“ bezeichnet. Unterhalb des Bruchstrichs steht der Divisor. Er wird in der Bruchrechnung als „Nenner“ bezeichnet.
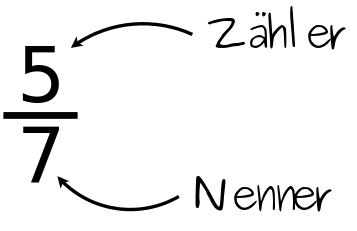
Ausgesprochen wird der Bruch, indem man den Zähler als Menge und den Nenner als Einheit benennt. Der Zahl im Nenner hängt man dafür die Silbe „-tel“ an. Der Bruch aus dem Beispiel wird also als „fünf Siebtel“ ausgesprochen.
Wie der Wert eines Bruches zustande kommt, kann man sich anhand eines praktischen Beispiels deutlich machen. Hierfür stellen wir uns vor, dass wir eine Torte aufteilen. Wir teilen sie in eine bestimmte Anzahl von Stücken auf (beispielsweise 8) und nehmen uns sechs dieser Stücke. Dann haben wir »sechs Achtel« der Torte. Die Anzahl der Stücke, in die die Torte insgesamt unterteilt wird, entspricht also dem Nenner und die Anzahl der Stücke, die wir erhalten, dem Zähler.
Im Folgenden werden einige Brüche in Bruchdarstellung und als Strecke abgebildet.
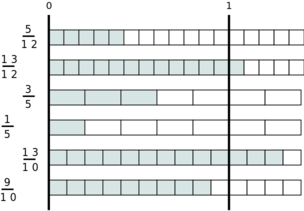
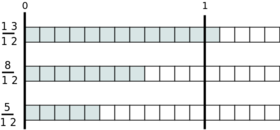
Wenn man Brüche vergleicht, muss man daran denken, dass der Zähler (steht über dem Bruchstrich) den Bruch größer macht, während der Nenner den Bruch kleiner macht. Das bedeutet, dass von zwei Bruchzahlen mit demselben Nenner der Bruch größer ist, dessen Zähler größer ist. So sind die nächsten drei Brüche der Größe nach sortiert. Anhand der Streckendarstellung erkennt man leicht, dass der Bruch mit dem größten Zähler auch den größten Wert hat.
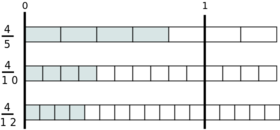
Umgekehrt verhält es sich bei Brüchen mit gleichem Zähler und unterschiedlich großem Nenner. Bei gleichem Zähler ist der Bruch am größten, der den kleinsten Nenner hat. Die nächsten drei Brüche haben alle denselben Zähler und sind wieder der Größe nach sortiert. In der Streckendarstellung erkennt man leicht, wie größere Nenner (d.h. kleinere Streckenabschnitte) zu kleineren Brüchen führen.
Beim Bruchrechnen steht man häufig vor dem Problem, dass zwei Bruchzahlen, die man vergleichen, addieren oder subtrahieren will, unterschiedliche Nenner haben. In diesen Fällen muss man den Nenner von einem oder beiden Brüchen ändern. Dies funktioniert, indem man den Bruch kürzt oder erweitert.
Um Brüche zu erweitern, werden einfach der Zähler und der Nenner mit derselben Zahl multipliziert. Der Bruch behält dabei seinen Wert, weil sich Zähler und Nenner um denselben Faktor ändern.
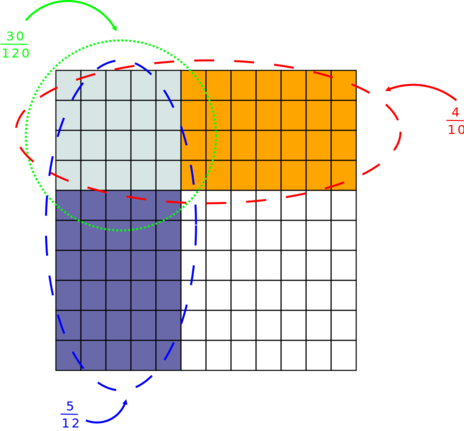
Die folgenden vier Brüche haben beispielsweise alle denselben Wert, auch wenn sie alle unterschiedliche Zähler und Nenner haben:
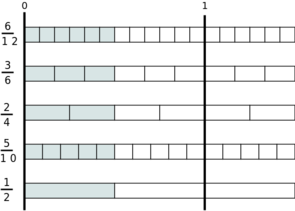
Beim Kürzen von Brüchen geht man den umgekehrten Weg wie beim Erweitern: Anstatt Zähler und Nenner mit derselben Zahl zu multiplizieren, dividiert man sie durch dieselbe Zahl. Dies geht natürlich nur, wenn Zähler und Nenner einen gemeinsamen Teiler haben. Wenn der Zähler und der Nenner keinen gemeinsamen Teiler mehr haben, ist es nicht möglich, den Bruch weiter zu kürzen. In diesem Fall spricht man von einem vollständig gekürztem Bruch.
Häufig steht man auch vor der Aufgabe aus einem Bruch einen vollständig gekürzten Bruch herzustellen. Hierfür sucht man nach dem größten gemeinsamen Teiler (ggT) von Zähler und Nenner und teilt beide Bestandteile des Bruches durch diese Zahl. Am einfachsten geht dies indem man alle Primfaktoren ermittelt, die gemeinsamen Primfaktoren multipliziert und Zähler und Nenner durch das Ergebnis teilt.
In der folgenden Tabelle sind für vier Brüche jeweils der größte gemeinsame Teiler und die Darstellung als vollständig gekürzter Bruch angegeben:
| Bruch |
ggT |
Vollständig gekürzter Bruch |
 |
3 |
 |
 |
4 |
 |
 |
3 |
 |
 |
4235 |
 |
Wie man vor allem an dem letzten Beispiel erkennt, kann die Darstellung von Brüchen durch das Kürzen oft erheblich vereinfacht werden.
Zwei Brüche können nur direkt verglichen, addiert oder subtrahiert werden, wenn sie nennergleich sind. In der Bruchrechnung steht man daher oft vor dem Problem, dass man zwei Brüche auf denselben Nenner bringen muss.
Im einfachsten Fall ist der Nenners des einen Bruchs ein Vielfaches des anderen. Dies ist beispielsweise bei den Brüchen 3/5 und 13/15 der Fall. Hier genügt es den Bruch mit dem kleineren Nenner um den Quotienten beider Nenner zu erweitert. So erhalten wir in dem Beispiel die beiden Brüche 9/15 und 13/15.
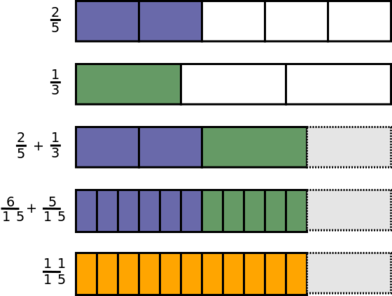
Falls keiner der beiden Nenner ein Vielfaches des anderen Nenners ist, muss man die Nenner beider Brüche anpassen. Dafür ermittelt man zuerst das kleinste gemeinsame Vielfache und bringt beide Brüche auf diesen Nenner. Hat man beispielsweise die beiden Brüche 3/4 und 5/6 ist das kleinste gemeinsame Vielfache der Nenner 12. Um 3/4 auf den Nenner 12 zu bringen, muss man mit 3 erweitern:

Und um 5/6 auf den Nenner 12 zu bringen, muss man mit 2 erweitern:

Oft ist es auch gar nicht notwendig, den kleinsten möglichen gemeinsamen Nenner zu finden. In vielen Fällen reicht es in der Bruchrechnung aus, überhaupt einen gemeinsamen Nenner zu haben. Dann kann man auch einfach jeden der beiden Brüche jeweils um den Nenner des anderen Bruches erweitern. Im Falle von 3/4 und 5/6 erhalten wir so:

und:

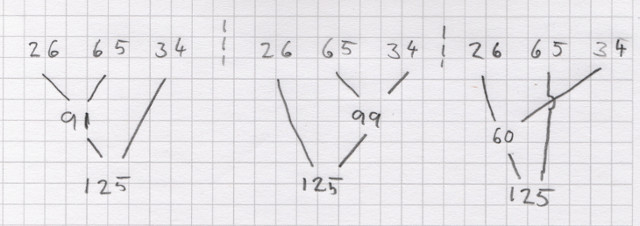
Brüche werden addiert oder subtrahiert, indem man sie zunächst nennergleich macht und anschließend ihre Zähler addiert oder subtrahiert. Diese Reihenfolge ist fundamental für die Bruchrechnung. Da hier eine Quelle für viele Fehler liegt, sollte sie jeder Schüler verinnerlichen: Nur nennergleiche Brüche dürfen addiert oder subtrahiert werden.
Wollen wir beispielsweise die Brüche 11/6 und 6/8 addieren, können wir folgendermaßen rechnen:

In der Bruchrechnung multipliziert man zwei Brüche, indem man sowohl ihre Zähler, als auch ihre Nenner jeweils miteinander multipliziert. Hierbei entstehen oftmals große Zahlen, weshalb die Ergebnisse soweit möglich gekürzt werden sollten. Andernfalls schleichen sich bei Folgerechnungen schnell Rechenfehler ein, da die Rechnungen sehr kompliziert werden.
Die Brüche 3/7 und 14/9 werden beispielsweise folgendermaßen multipliziert:

Bei sehr großen Zähler und Nenner, kann man auch vor der eigentlichen Multiplikation bereits mit dem Kürzen beginnen. Hierfür schreibt man Zähler und Nenner jeweils als Produkte ihrer Primfaktoren und streicht anschließend alle Faktoren, die sowohl im Zähler als auch im Nenner vorkommen. So multipliziert man die Brüche 60/77 und 22/15 beispielsweise so:

Die Division von zwei Brüchen ist nicht viel schwieriger als die Multiplikation. So wird ein Bruch durch einen anderen dividiert, indem man ihn einfach mit dessen Kehrwert multipliziert. Der Kehrwert (oder auch das Inverse) eines Bruches beschreibt die Zahl, mit der man ihn multiplizieren muss, damit er zu 1 wird. Man kann ihn ganz einfach ermitteln, indem man einfach Nenner und Zähler vertauscht. Von 3/4 ist beispielsweise 4/3 der Kehrwert und von 12/7 ist es 7/12.
Will man den Bruch 5/8 durch 3/4 teilen rechnet man also: