- Übersicht über die wichtigsten Formeln der Zinsrechnung
- Grundbegriffe der Zinsrechnung
- Jahreszins: Zinsen für ein Jahr berechnen
- Zinsen für einzelne Monate oder Tage berechnen
- Zinseszins
- Zinsen bei jährlicher Einzahlung mit Zinseszinsrechnung
- Zinssätze berechnen
Zinsrechnung ist angewandte Prozentrechnung. Wir benötigen die Zinsrechnung überall, wo wir mit Zinsen rechnen – insbesondere, wenn wir die Kosten für einen Kredit oder den Gewinn aus einer Geldanlage berechnen wollen. In diesem Artikel erfährst du anhand von Beispielen und Erklärungen zur Zinsrechnung, wie du praktisch mit Zinsen rechnest. Wenn du dich noch nicht so gut mit der Prozentrechnung auskennst, lies dir zuerst die Seiten zur Prozentrechnung und zum Dreisatz durch. Dort lernst du Begriffe wie Prozentsatz, Grundwert und Prozentwert kennen, die du für die Zinsrechnung benötigst.
Übersicht über die wichtigsten Formeln der Zinsrechnung
Hier findest du eine knappe Übersicht über die wichtigsten Formeln der Zinsrechnung. Weiter unten auf der Seite stehen die detailierten Erklärungen zu den Formeln.
| Formel | Bedeutung |
|---|---|
| Jahreszins | |
| Tageszins (Deutsche Methode) | |
| Monatszins (Deutsche Methode) | |
| Endkapital nach einer Zinsperiode | |
| Endkapital mit Zinseszinsen | |
| Sparkassenformel |
Grundbegriffe der Zinsrechnung
- Zinssatz: Der Zinssatz wird als Prozentsatz angegeben und beschreibt, wie viele Zinsen abhängig vom Kapital für einen bestimmten Zeitraum (die Zinsperiode) gezahlt werden. In den Formeln geben wir den Zinssatz als p an.
- Kapital: Als Kapital bezeichnen wir die angelegte Geldmenge, für die Zinsen gezahlt werden. Zahlt man beispielsweise 100 Euro auf ein Sparkonto ein, sind diese 100 Euro das Anfangskapital. Wenn wir nicht mit einer Geldanlage, sondern mit einem Kredit rechnen, ist die geliehene Geldsumme das Kapital. In den Formeln geben wir das Kapital als K und das Endkaptial als Z an.
- Zinsperiode: Zinsen werden immer für einen bestimmten Zeitraum bezahlt. Die Zeit, für die ein Zinssatz angegeben wird, nennt man Zinsperiode. In der Zinsrechnung betrachtet man üblicherweise einen Jahreszins. Weiter unten zeigen wir, wie man rechnen muss, wenn man einen anderen Zeitraum als die Zinsperiode betrachtet.
Zu dem Begriff „Zinssatz“ noch eine wichtige Anmerkung: Außer „Zinssatz“ hört man in der Zinsrechnung manchmal den Begriff „Zinsfuß“. Dabei bezeichnet der Zinsfuß die Zahl vor dem Prozentzeichen und der Zinssatz entspricht dem Prozentsatz. Falls wir also einen Zinssatz von 2,5 % = 0,025 haben, ist der Zinsfuß 2,5.
Jahreszins: Zinsen für ein Jahr berechnen
Im einfachsten Fall ermittelt man mit der Zinsrechnung, wie viele Zinsen man für sein Anfangskapital in einer Zinsperiode erhält oder wie viele Zinsen man für einen Kredit in einer Zinsperiode zahlt. Da die Zinsperiode in der Zinsrechnung üblicherweise ein Jahr beträgt, berechnet man also den Jahreszins.
Die Zinsen errechnen sich aus dem Produkt aus Zinssatz (p) und Anfangskapital (K). Die Formel lautet:
Auf die Prozentrechnung übertragen, entspricht der Jahreszins dem Prozentwert des Zinses (Prozentsatz) bezogen auf das Kapital (Grundwert).
Möchte man wissen, wie sich der Wert des angesparten Gelds nach einem Jahr entwickelt hat, addiert man zum Jahreszins den ursprünglichen Kapitalwert und erhält das sogenannte Endkapital. Alternativ addiert man zum Zinssatz einhundert Prozent. Die Formel für das Endkapital lautet daher:
Beispiel: Angenommen wir legen 400 Euro zu einem Zinssatz von 2,25 % für ein Jahr an. Wir erhalten nach einem Jahr folgende Zinsen ausgezahlt:
Der Wert des Endkapitals beträgt:
Zinsen für einzelne Monate oder Tage berechnen
Manchmal möchte man Zinsen nicht für ein ganzes Jahr, sondern für einen kürzeren Zeitraum berechnen. Die Zinsrechnung bietet verschiedene Möglichkeiten, den Zinssatz auf einzelne Tage herunterzurechnen. Die sogenannten „Deutschen Methode“ rechnet für das ganze Jahr mit 360 Tagen und für jeden Monat mit 30 Zinstagen. Sie unterscheidet sich von der tagegenauen Methoden, die mit der tatsächlichen Anzahl von Tagen pro Jahr (365, beziehungsweise 366 in Schaltjahren) und pro Monat rechnet. Wir stellen hier die „Deutsche Methode“ der Zinsrechnung genauer vor.
Zur Berechnung der Tageszinsen nutzt man in der Zinsrechnung den einfachen Dreisatz. Berechnet man mit der „Deutschen Methode“, teilt man den Zinssatz durch 360, um den Zinssatz pro Tag zu erhalten. Diese Tageszinsen multipliziert man mit der Anzahl der Tage. So berechnet man die Zinsen für mehrere Zinstage (t) so:
Werden also 200 Euro für 24 Tage zu einem Zinssatz von 4 Prozent verzinst, erhält man Zinsen in Höhe von:
Auch andere Zinsperioden werden in der Zinsrechnung auf diese Weise berechnet. Die Gleichung zur Berechnung der Monatszinsen lautet beispielsweise:
Zinseszins
Wenn man Geld über einen längeren Zeitraum anlegt und die Zinsen nicht abhebt, sondern ebenfalls anspart, erhält man in den folgenden Jahren nicht nur auf den ursprünglich eingezahlten Betrag Zinsen, sondern auch auf die früheren Zinsen. Zinsen, die auf Zinsen gezahlt werden, bezeichnet man in der Zinsrechnung als Zinseszins.
Die folgende Tabelle zeigt an einem Beispiel der Zinseszinsrechnung, wie Zinseszinsen den gesparten Betrag erhöhen. In diesem Beispiel wird ein Kapital von 300 Euro auf ein Sparkonto mit vierprozentiger Verzinsung eingezahlt. Die mittlere Spalte zeigt den Wert des Kapitals mit und die recht Spalte den Wert ohne Zinseszins
| Jahr | Mit Zinseszins | Ohne Zinseszins |
|---|---|---|
| 1 | 300 Euro | 300 Euro |
| 2 | 312 Euro | 312 Euro |
| 3 | 324,48 Euro | 324 Euro |
| 4 | 337,46 Euro | 336 Euro |
| 5 | 350,96 Euro | 348 Euro |
| 6 | 365 Euro | 360 Euro |
| 7 | 379,60 Euro | 372 Euro |
| 8 | 394,78 Euro | 384 Euro |
| 9 | 410,57 Euro | 396 Euro |
| 10 | 426,99 Euro | 408 Euro |
| … | ||
| 50 | 2.050 Euro | 888 Euro |
Der Zinseszins hat in diesem Beispiel das Kapital über fünfzig Jahre beinahe versiebenfacht. Bei einfacher Verzinsung ist das Endkapital lediglich knapp dreimal so groß wie der Geldbetrag, den man angelegt hat.
In der Zinseszinsrechnung steigt der Wert des Kapitals exponentiell. Die folgende Grafik zeigt wie sich der Wert des angelegten Geldes aus dem obigen Beispiel mit der Zeit entwickelt. Die grüne Line zeigt was das Kapital bei einfacher Verzinsung nach einer bestimmen Zahl an Jahren Wert ist, die rote Line zeigt die Entwicklung des Kapitals mit Zinseszinsen:
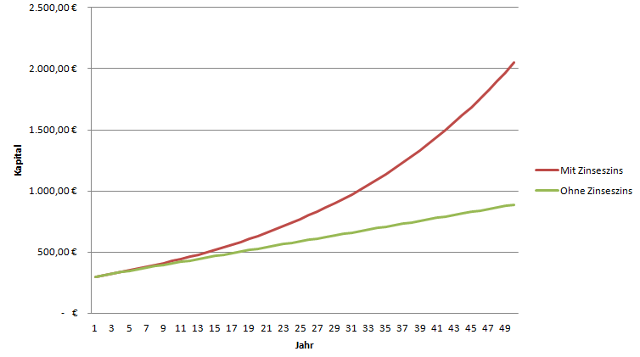
Um die Verzinsung mit Zinseszins zu berechnen, nutzt man folgende Formel:
In dieser Formel steht K für das Anfangskapital, Z für das Endkapital, p für den Zinssatz und t für die Anzahl der Zinsperioden.
Zinsen bei jährlicher Einzahlung mit Zinseszinsrechnung
Bei längerfristigen Sparplänen ist es üblich, nicht nur einen anfänglichen Geldbetrag anzulegen, sondern zusätzlich jährlich einen festgelegten Betrag einzuzahlen. Diesen Betrag bezeichnet man in der Zinsrechnung als Annuität. In allen Folgejahren wird er ebenfalls verzinst.
Der Wert des Endkapitals wird mit der sogenannten Sparkassenformel berechnet:
In der Sparkassenformel steht wie in der Zinsrechnung üblich K für das Anfangskapital, Kn für die Annuität, Z für das Endkapital und q für 1 + p.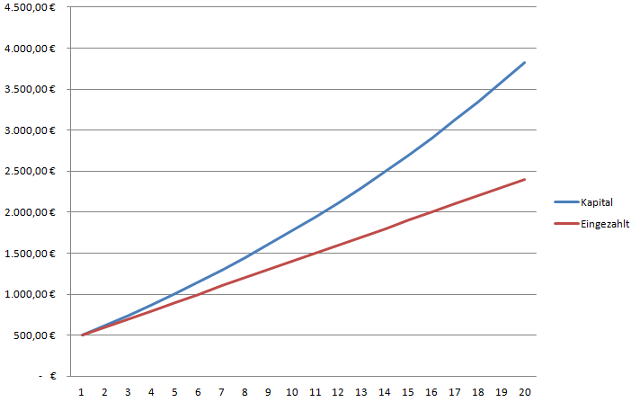
Diese Grafik, zeigt die Kapitalentwicklung, bei einmaliger Einzahlung von 500 Euro und einer jährlichen Einzahlung von 100 Euro bei 4 Prozent Zinsen. Nach 20 Jahren wurde ein Betrag von 2.400 Euro eingezahlt, der mit Verzinsung auf 3.820,55 Euro angewachsen ist.
Zinssätze berechnen
In den bisherigen Formeln der Zinsrechnung waren Zinssatz, Kapital und die Zinsperioden gegeben. Manchmal kennt man jedoch statt des Zinssatzes nur das Endkapital. Die Frage, die man damit beantwortet, lautet beispielsweise: „Zu welchem Zinssatz muss ich 100 Euro anlegen, damit daraus nach zehn Jahren 400 Euro werden?“.
Die Formel zur Berechnung des Zinssatzes mit dem Endkapital Z und dem angelegten Betrag K lautet bei einer Zinsperiode von einem Jahr:
Und bei mehrjähriger Verzinsung:
Die oben gestellte Frage beantwortet die Zinseszinsrechnung mit:
Man muss das Kapital also über zehn Jahre mit knapp fünfzehnprozentiger Verzinsung anlegen, um auf das angestrebte Endkapital zu kommen.
